Den skjulte fellen - Evolusjonens skallspill
Av William A. Dembski, 10. januar 2025. Oversatt herfra

Forfatterens merknad: Bevaring av informasjon -lenke, er et stort resultat av den intelligente designlitteraturen, selv om det til dags dato ikke har fått den oppmerksomheten den fortjener. Det kvantifiserer mengden informasjon som trengs for å øke sannsynligheten for å finne en nål i en høystakk slik at nålen faktisk kan bli funnet. Resultatet av bevaring av informasjon, er at informasjonen som trengs for å finne en nål i en høystakk, på sin side krever å finne en annen nål i en høystakk, noe som antyder at det ikke er noen gratis lunsj i søk. Jeg har nettopp skrevet opp en full redegjørelse for bevaring av informasjon for tidsskriftet Bio-Complexity i en artikkel med tittelen "The Law of Conservation of Information: Natural Processes Only Delistribute Excising Information." Det som følger er et avsnitt fra artikkelen om forskyvnings-feilen. Denne delen er tilgjengelig og hjelper til med å tydeliggjøre intuisjonene som ligger til grunn for bevaring av informasjon.

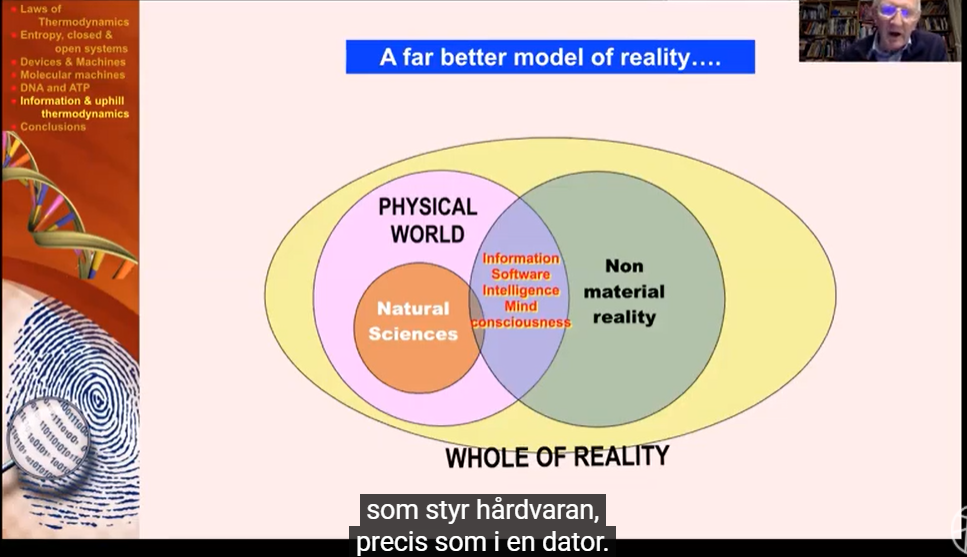
Bilde 1. Hva består virkeligheten av?

Oppdagelsen av bevaring av informasjon startet ikke med å bevise et matematisk teorem. Snarere kom oppdagelsen fra gjentatte ganger å legge merke til hvordan innsatsen for å redegjøre for suksessen til søk, hvis sjanse for suksess tilsynelatende var håpløst, alltid smuglet inn informasjon som det ikke ble redegjort for. Ett hull ble fylt, men bare ved å grave et annet, og så et nytt hull som så på sin side måtte forklares. Denne forklaringen ble spesielt tydelig i evolusjonslitteraturen. Darwinistiske tilnærminger til biologisk evolusjon og evolusjonær databehandling forsøkte å forklare opprinnelsen til informasjon gjennom en eller annen prosess som direkte brukte eller ellers etterlignet naturlig utvalg. Likevel snarere enn å innrømme et grunnleggende gap i forklaringen, påkalte denne litteraturen ganske enkelt naturlig utvalg som en bakenforliggende grunn for å forklare opprinnelsen til informasjon, og denne bakenforliggende årsaken er fritatt for ytterligere forklaring.

Flyttingen for å forklare opprinnelsen til informasjon ved å påberope seg en separat uforklarlig informasjonskilder, typisk via en utvelgelsesprosess, var så vanlig i den evolusjonære litteraturen at den fortjente sitt eget navn: forskyvning. (1) Forskyvning ble det valgte verktøyet blant evolusjonære kritikere av Intelligent design da de prøvde å ugyldiggjøree logikken i designslutningen, som utledet design for både spesifiserte og usannsynlige hendelser. Kritikere hevdet at når naturlig utvalg kom i spill, fungerte det som en sannsynlighetsforsterker som fjernet enhver tilsynelatende usannsynlighet, som ellers kunne ha stått for en gyldig designslutning. Følgelig hevdet kritikere at tilsynelatende designprodukter kunne bortforklares gjennom evolusjonsprosesser, som ikke krever design. (2)

Usannsynlige produkter
Men dette forsøket på å ugyldiggjøre designslutningen var for enkelt. Produkter kan utformes, men også prosesser som bygger produkter kan utformes (sammenlign en Tesla -bil med en Tesla -fabrikk som bygger Tesla -biler - begge er designet). Design -slutningen gir mening for usannsynlige produkter. Bevaring av informasjon, gjennom søket etter et søk, gir mening til usannsynlige prosesser som gir ut sannsynlige produkter. å gi mening til forskyvning var et avgjørende skritt for å utvikle en presis matematisk behandling av bevaring av informasjon.

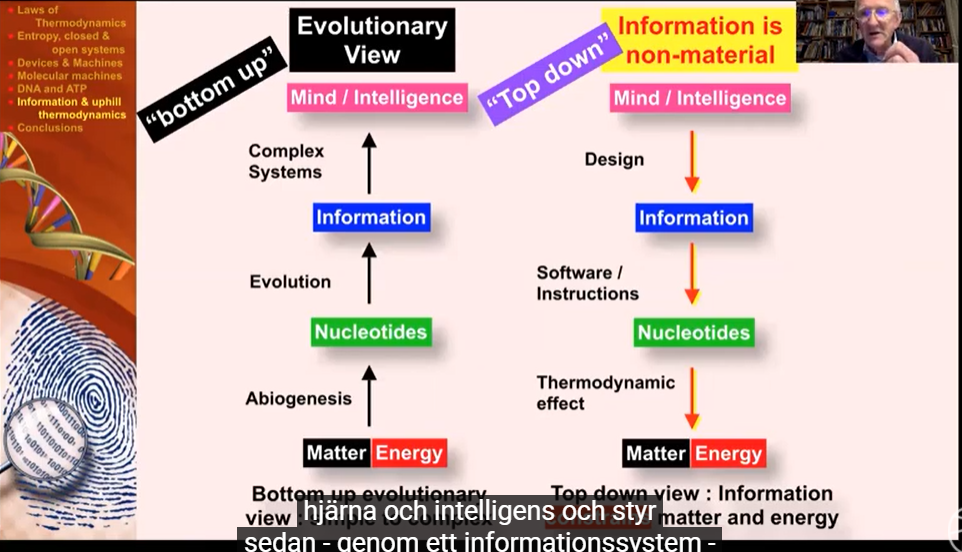
Bilde 2. Konsekvens: enten bottom-up eller top-down

Mens bevaring av informasjon var et matematisk bekreftet teoretisk funn, var forskyvning et induktivt bekreftet empirisk funn. Om og om igjen ble informasjon som visstnok ble opprettet fra bunnen av, i det skjulte introdusert under pretensjonen om at informasjonen allerede var tilstrekkelig forklart, da den faktisk bare ble forutsatt. Faktisk ble forskyvning et spesial tilfelle av feilen ved å tigge spørsmål, som skjulte snarere enn belyste, evolusjonsprosesser.

Bilde 3. Logiske lover -har også sitt opphav

Et av de mer modige eksemplene på forskyvning som jeg personlig møtte, skjedde i et intervju fra 2001 med darwinist Eugenie Scott på Peter Robinsons program: Uncommon Knowledge. Scott og jeg diskuterte evolusjon og intelligent design da Robinson løftet påstanden om at en ape, gitt nok tid, ville produserte verkene til Shakespeare ved å skrive tilfeldig på en skrivemaskin. Scott svarte med å si at i motsetning til dette eksemplet, der apenes skriving bare produserer tilfeldig variasjon, er naturlig utvalg lik en tekniker som står bak apen og fjernet hver feil apen gjorde ved å skrive Shakespeare.(3). Men hvor finner du en tekniker som vet nok om verkene til Shakespeare for å luke ut feil i skrivingen av Shakespeare? Hva er kvalifikasjonene til denne teknikeren? Hvordan vet teknikeren hva han skal slette? Scott sa det aldri. Det er forskyvning: apenes suksess med å skrive Shakespeare blir forklart, men på bekostning av å forlate teknikeren, som korrigerer apen som skriver, uforklart.

Om den røyskatten
I sin bok The Blind Watchmaker hevder Richard Dawkins å vise hvordan naturlig utvalg kan skape informasjon ved å appellere til hans velkjente METHINKS IT IS LIKE A WEASEL -datasimulering.(4) Ren tilfeldig prøvetaking av de 28 bokstavene og rommene i denne målfrasen ville ha En sannsynlighet på bare 1 av 27^28, eller omtrent 1 til 10^40, for å oppnå den. Ved å utvikle METHINKS IT IS LIKE A WEASEL, var Dawkins simulering i stand til å overvinne denne usannsynligheten ved nøye å velge et egnethetslandskap for å tilordne høyere egnethet til karaktersekvenser som har flere tilsvarende bokstaver til felles med målfrasen.

I stedet for ren tilfeldighet, erstattet Dawkins en algoritme med bakkeklatring med nøyaktig en topp og med en klar måte å forbedre egnetheten hvor som helst borte fra toppen (glatte og økende gradienter hele veien!). (5) Men hvor kom dette egnethetslandskapet fra? Et slikt egnethetslandskap eksisterer for enhver mulig målfrase overhodet, og ikke bare for å tømme at det er som en weasel. Dawkins forklarer utviklingen av å tømme at det er som en weasel når det gjelder et egnethets-landskap som med høy sannsynlighet gir sannsynlighet for evolusjon til å nå denne målfrasen. Likevel forlater han egnethetslandskapet i seg selv uforklart. (6) På den måten begår han en forskyvningsfeil. (7)

Forskyvning er også tydelig i arbeidet til Dawkins når han skifter fra datasimuleringer til biologisk evolusjon. Faktisk kan hele boken hans: Climbing Mount Improbable, sees på som en øvelse i forskyvning som anvendt på biologi.(8) I den boken sammenligner Dawkins fremveksten av biologisk kompleksitet med å klatre på et fjell. Han kaller det Mount Improbable fordi hvis du måtte komme helt til toppen i med en gang (det vil si oppnå en massiv økning i biologisk kompleksitet på en gang), ville det være svært usannsynlig. Men må Mount Improbable bestiges i ett sprang? Darwinismen hevder å vise hvordan Mount Improbable kan skaleres i små trinnvise steg. I følge Dawkins har Mount Improbable alltid en gradvis buktende sti som fører til toppen, som kan bestiges i baby-trinn.

Men hvor er verifiseringen av denne påstanden? Det kan være at Mount Improbable er bratt på alle sider, og at å komme til toppen via baby-trinn effektivt er umulig. Følgelig er det ikke nok til å forutsette at en egnethetsøkende sekvens av babytrinn alltid kobler biologiske systemer. En slik forbindelse må påvises, og til dags dato er den ikke det, som Michael Behes arbeid med ikke-reduserbar kompleksitet viser. (9) Men selv om en slik forbindelse kunne demonstreres, hva ville dette si om forholdene for dannelsen av Mount Improbable i utgangspunktet?
Fjell blir tross alt ikke til på magisk vis - de må dannes av en viss prosess av fjelldannelse. Av alle de forskjellige måtene som Mount Improbable kan ha dukket opp på, hvor mange er stupbratte, slik at det ikke eksisterer noen gradvis vei til toppen? Og hvor mange tillater en gradvis vei til toppen? Et Mount Improbable med gradvise stier til toppen, kan i seg selv være usannsynlig. Dawkins antar ganske enkelt at Mount Improbable må være slik at det letter darwinistisk evolusjon. Men på den måten begår han en forskyvningsfeil, forutsetter hva som må forklares og rettferdiggjøres, og gjør dermed illegitimt et problem til sin egen løsning.(10)

Bilde 4. Liten gutt om bekreftelsesavvik

Eksempler på forskyvning
I den evolusjonære databehandlingslitteraturen kan eksempler på forskyvning mer sofistikert enn Dawkins røyskatt lett finnes. Men den samme spørsmål-tiggende forskyvningsfeilen ligger til grunn for alle disse eksemplene. Den mest publiserte forekomsten av forskyvning i den evolusjonære databehandlingslitteraturen dukket opp i Nature tilbake i 2003. Richard Lenski, Charles Ofria, Robert Pennock og Christoph Adami hadde utviklet en datasimulering kalt Avida. (11) De hevdet at denne simuleringen var i stand til å lage komplekse Boolske operatører uten spesielle innspill eller kunnskap. En av medforfatterne, Pennock, gikk deretter videre for å hevde at Avida avgjørende tilbakeviste Michael Behes arbeid med ikke-reduserbar kompleksitet.(12) og gitt at ikke-reduserbar kompleksitet er i kjernen av intelligent design, hevdet i virkeligheten at Avida også hadde tilbakevist intelligent design.

Men som Winston Ewert og George Montañez viste ved å spore informasjons-strømmen gjennom Avida, overskred mengden informasjon som kom ut, gjennom nydannede komplekse boolske operatører, aldri mengden av informasjon som ble lagt inn i den. Faktisk var Avida jury-rigget for å produsere selve kompleksiteten den hevdet å produsere gratis: Avida belønnet stadig økende kompleksitet bare for kompleksitetens skyld, og ikke av uavhengige funksjonelle grunner. Andre eksempler som Thomas Schneiders EV, Thomas Ray's Tierra og David Thomas Steiner Tree Search -algoritme fulgte alle det samme mønsteret. Ewert og Montañez var i stand til å vise nøyaktig hvor informasjonen som visstnok ble opprettet fra bunnen av i disse algoritmene, faktisk hadde blitt innebygd fra begynnelsen. (14) Forskyvning, som forskningen deres viste, er gjennomgripende i denne litteraturen.

Det empiriske arbeidet med å vise forskyvning for disse datasimuleringene setter scenen for det teoretiske arbeidet med bevaring av informasjon. Disse simuleringene, og deres jevnlige unnlatelse av å forklare opprinnelsen til informasjon, førte til en undersøkelse av den nøyaktige numeriske sammenhengen mellom informasjonsinnlegget og informasjonsutgangen. Å vise forskyvning startet lik en fra gang til gang anstrengelse, for å avdekke nøyaktig hvor informasjon hadde blitt smuglet inn i en datasimulering. Når matematikken for bevaring av informasjon ble utviklet, var imidlertid behovet for å finne nøyaktig hvor informasjonen ble smuglet inn, ikke lenger så viktig, da teorien steppet inn der observasjon kom til kort.

Duehull prinsippet
Teorien garanterte at informasjonen ble smuglet inn, selv om de evolusjonære simuleringene ble så bysantinske at det var vanskelig å følge dens nøyaktige informasjonsflyt. Analogt, hvis du har hundre og ett brev som må legges inn i hundre postkasser, garanterer due-hullsprinsippet i matematikk at en av postkassene må ha mer enn ett brev. (15) Kontroll av dette empirisk kan være vanskelig, om ikke praktisk talt umulig, på grunn av alle de mange mulige måtene disse brevene kan fylle postkassene. Teorien kommer i dette tilfellet til unnsetning, og garanterer hva observasjon alene ikke kan.

Bilde 5. Hvem det hele stammer fra

Forskyvning er et skallspill. I et skallspill plasserer en operatør en liten gjenstand, som en ert, under en av tre kopper og stokker deretter raskt koppene for å forvirre observatører om objektets beliggenhet. Deltakerne blir invitert til å gjette hvilken kopp som skjuler erten, men spillet er ofte avhengig av fingerferdighet, og villedning for å øke sannsynligheten for at deltakerne gjetter feil. Så lenge spillet spilles rettferdig, er erten under en kopp og forblir under en kopp. Det kan ikke magisk materialisere eller dematerialisere. Spillet kan bli mer sofistikert ved å øke antallet kopper og ved at operatøren flytter koppene med større hastighet og smidighet. Men ved å spore operatøren nøye, er det alltid mulig å avgjøre hvor erten startet og hvor den havnet. Ertens plassering her tilsvarer informasjon. Forskyvning sier at den alltid var der. Bevaring av informasjon gir den underliggende matematikken for å demonstrere at den faktisk alltid var der.

Video: Magisk trick -lenke.

Bilde 6. En kjent illusjons-trick

Referanser -se slutten av originalartikkelen -lenke.

William A. Dembski Bilde 7; Medlem av Styret, Discovery Institute
Bill Dembski er en matematiker og filosof, og er forfatter/redaktør av mer enn 25 bøker, samt forfatter av fagfellevurderte artikler som spenner over matematikk, ingeniørvitenskap, biologi, filosofi og teologi. Med doktorgrad i matematikk (University of Chicago) og filosofi (University of Illinois i Chicago), er Bill en aktiv forsker innen intelligent design. Men han er også en teknisk gründer som bygger pedagogisk programvare og nettsteder, og utforsker hvordan utdanning kan bidra til å fremme menneskelig frihet ved hjelp av teknologi.

Oversettelse, via google oversetter, og bilder ved Asbjørn E. Lund